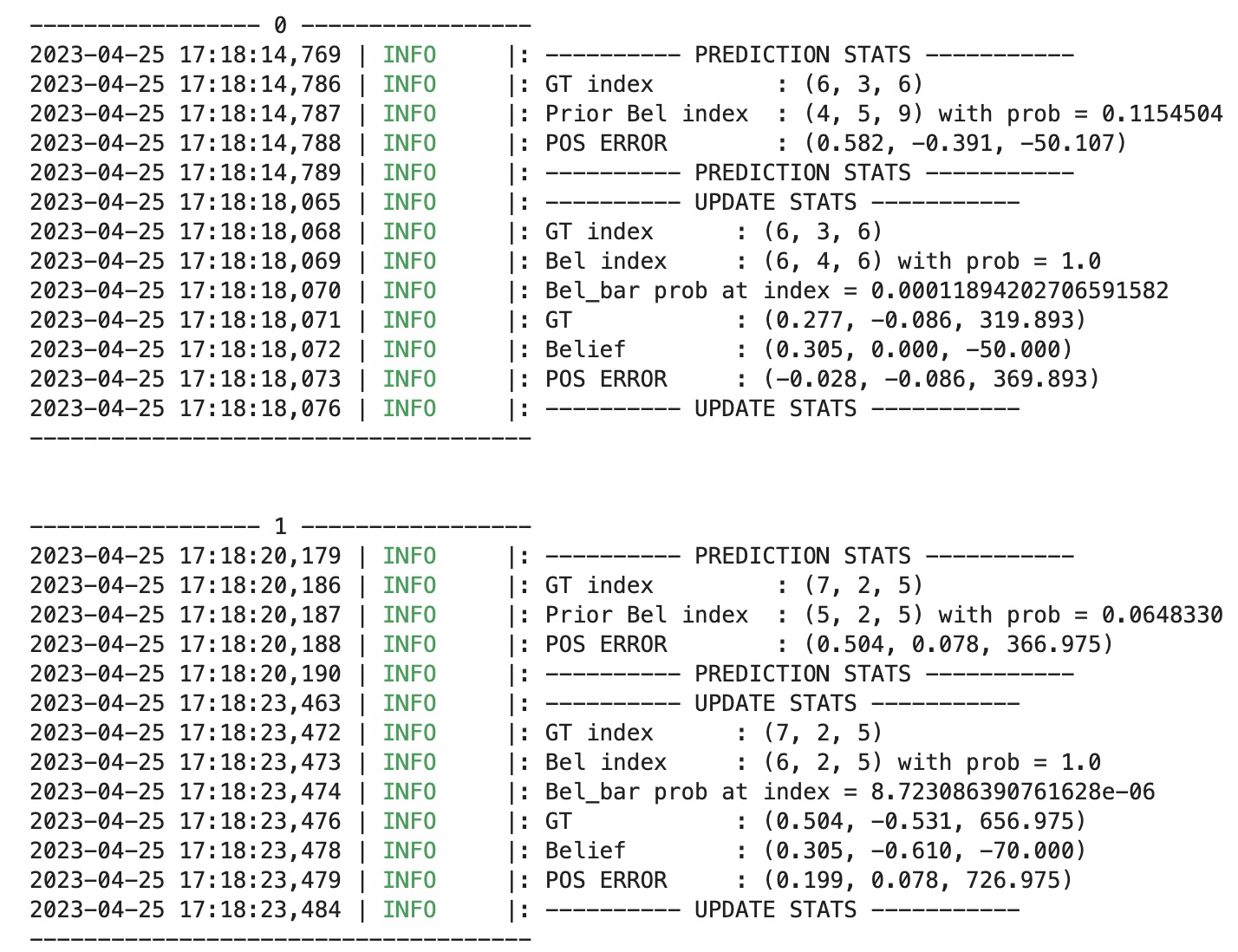
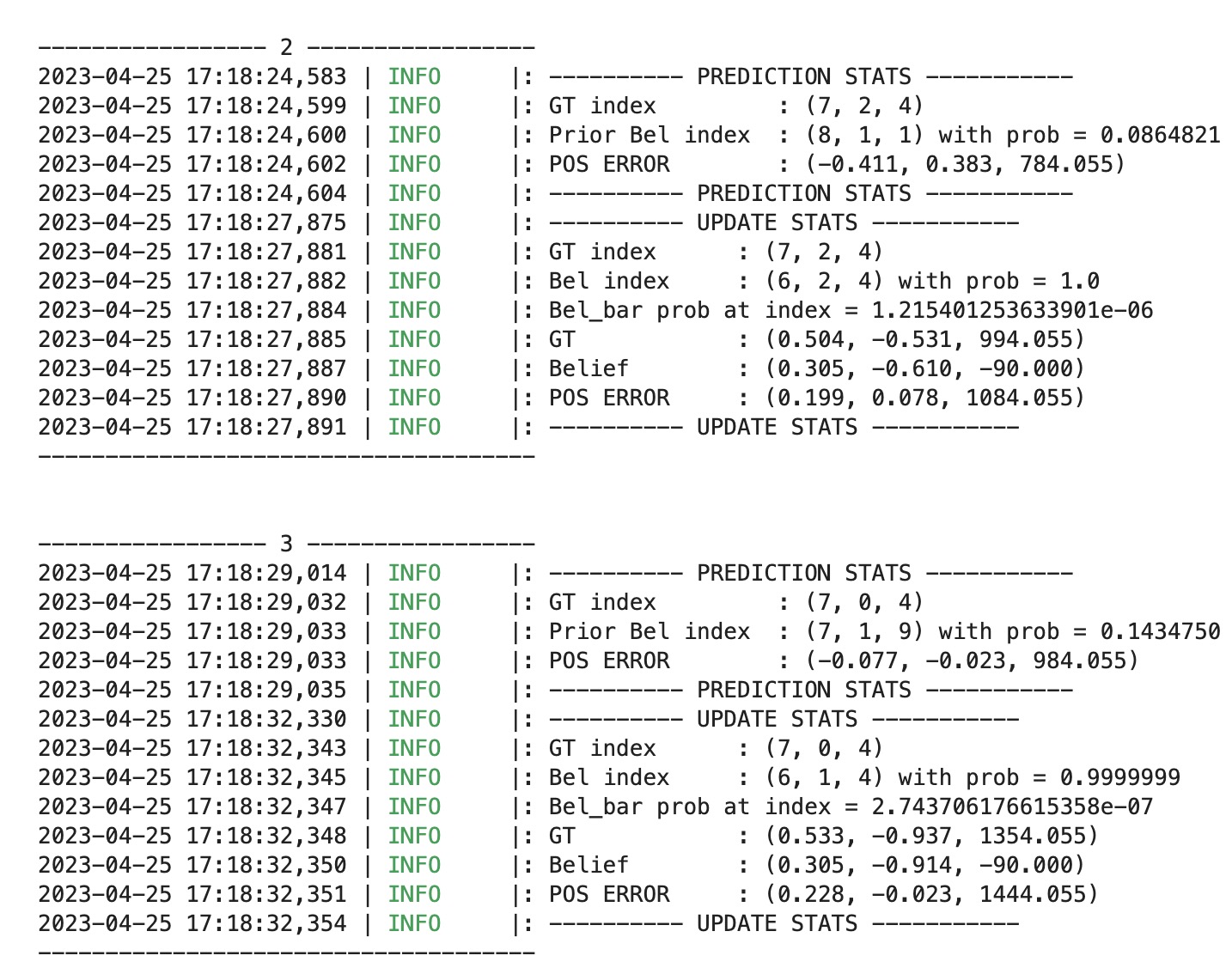
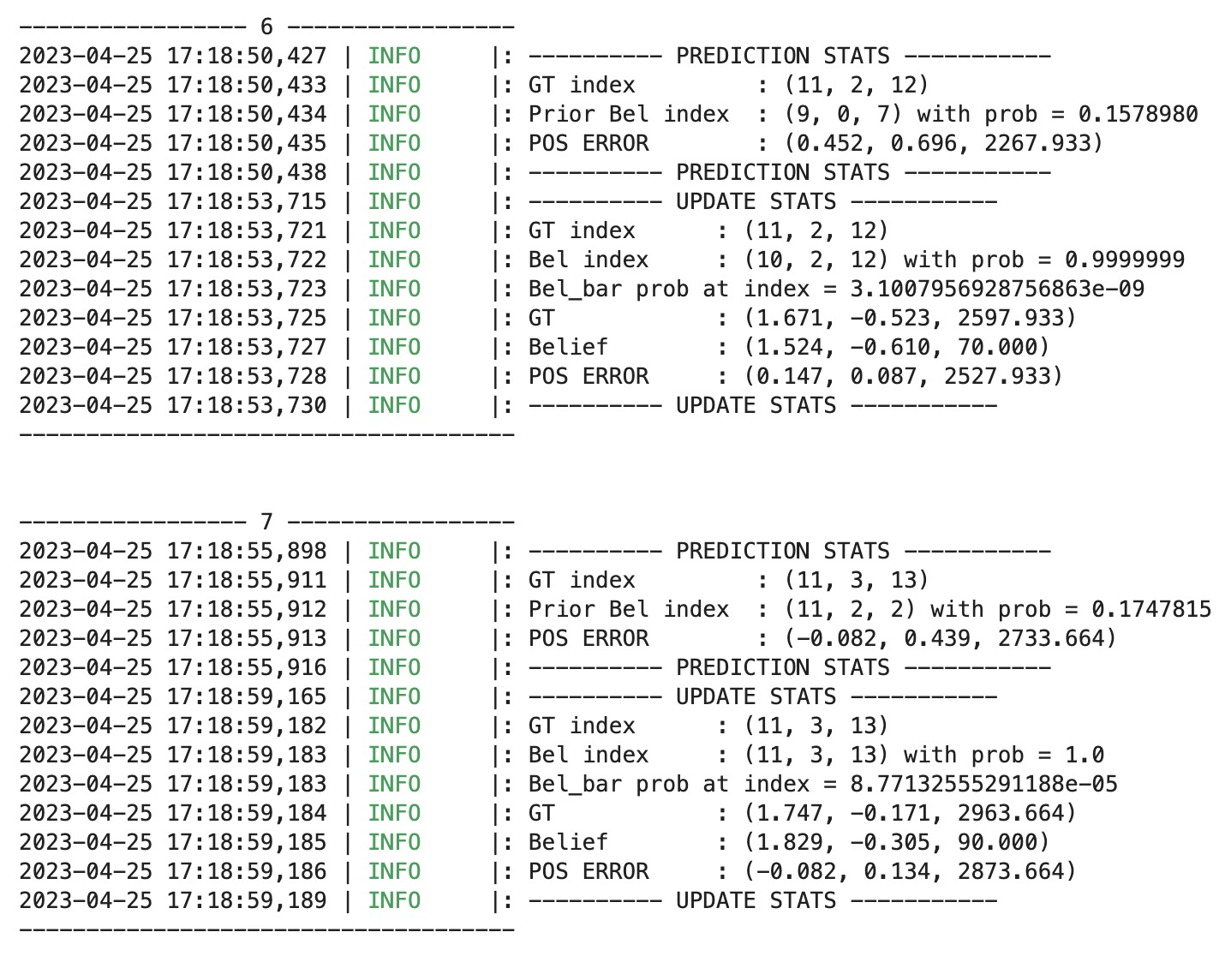
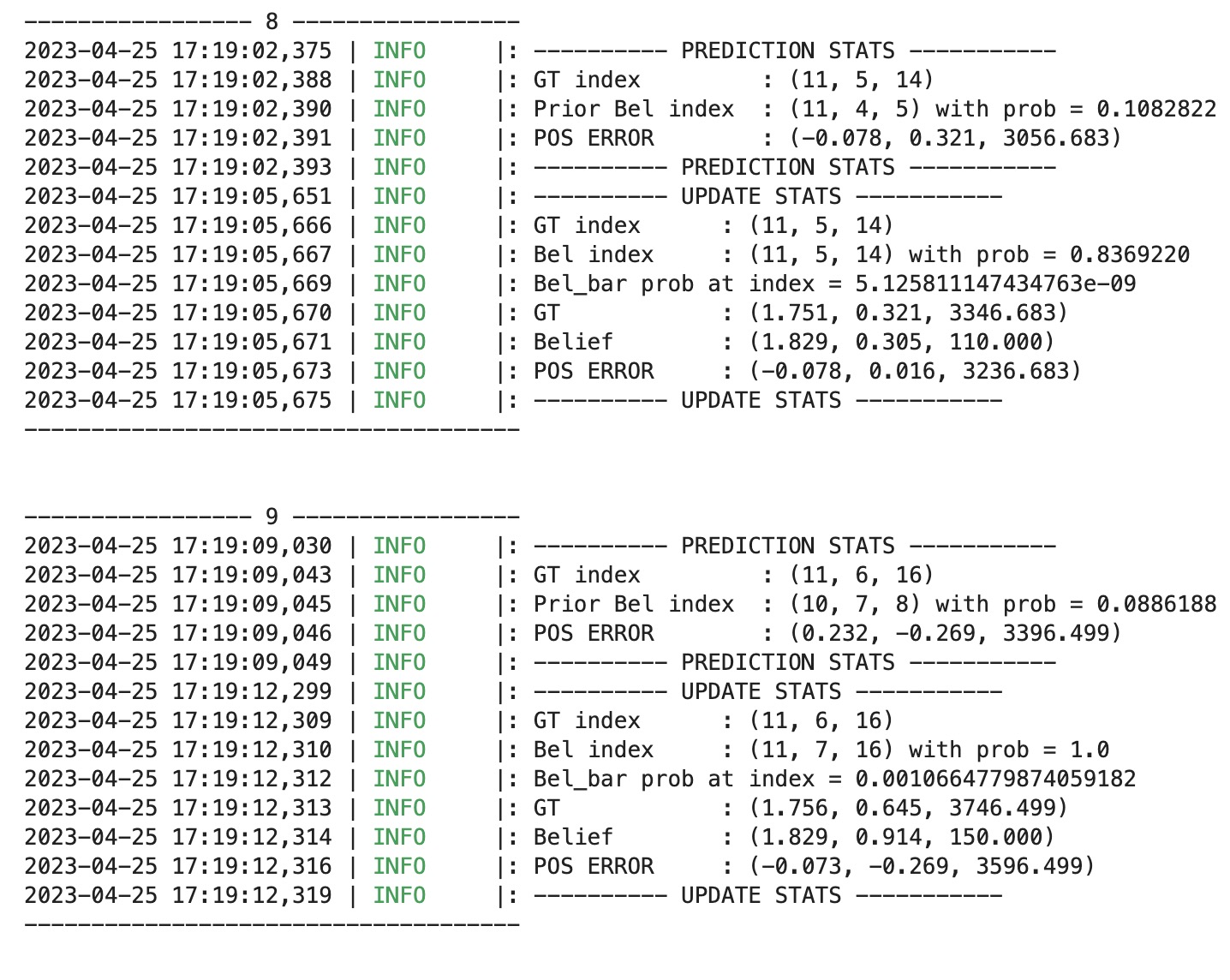
Lab 10 - Localization (sim)

Pre-lab

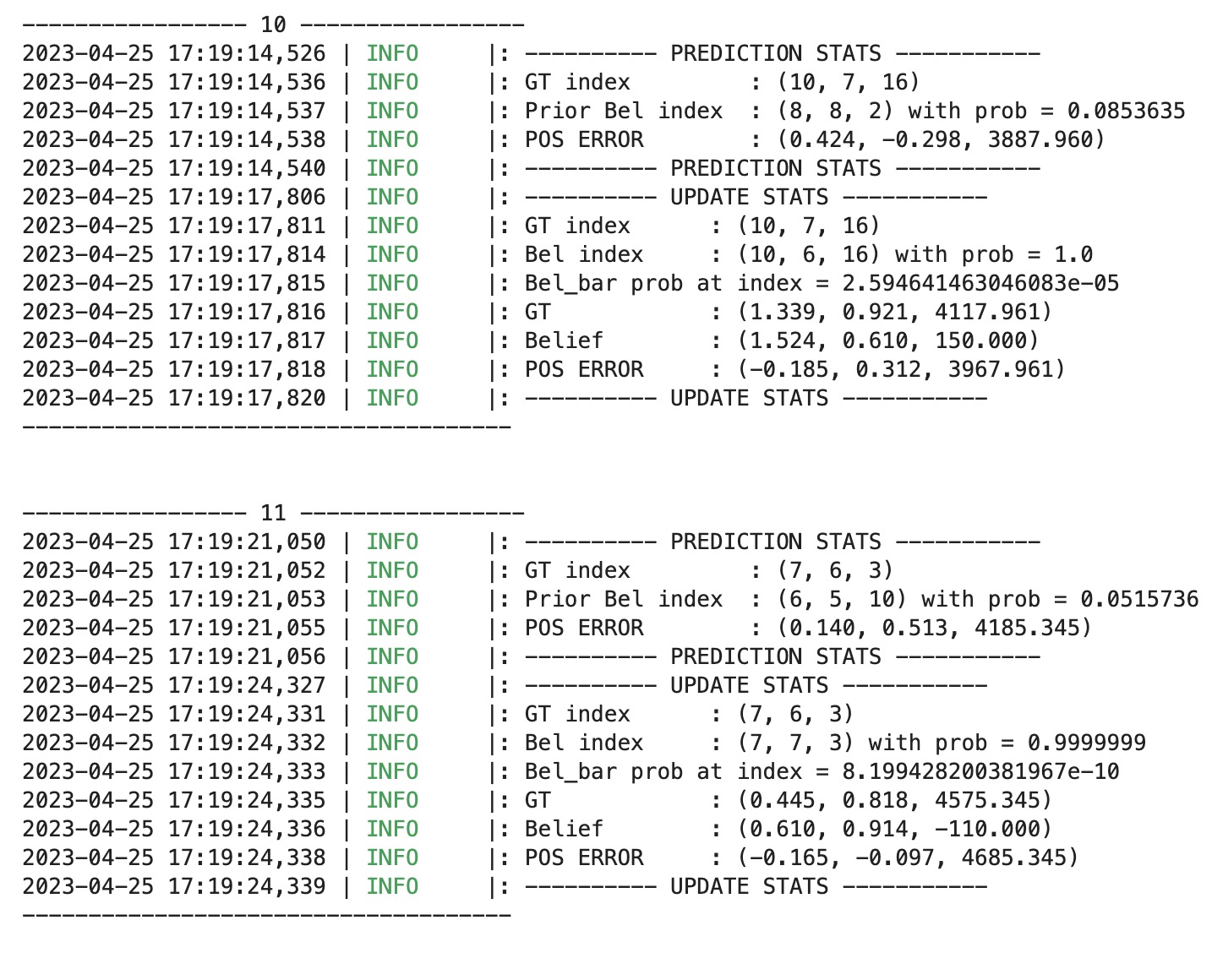
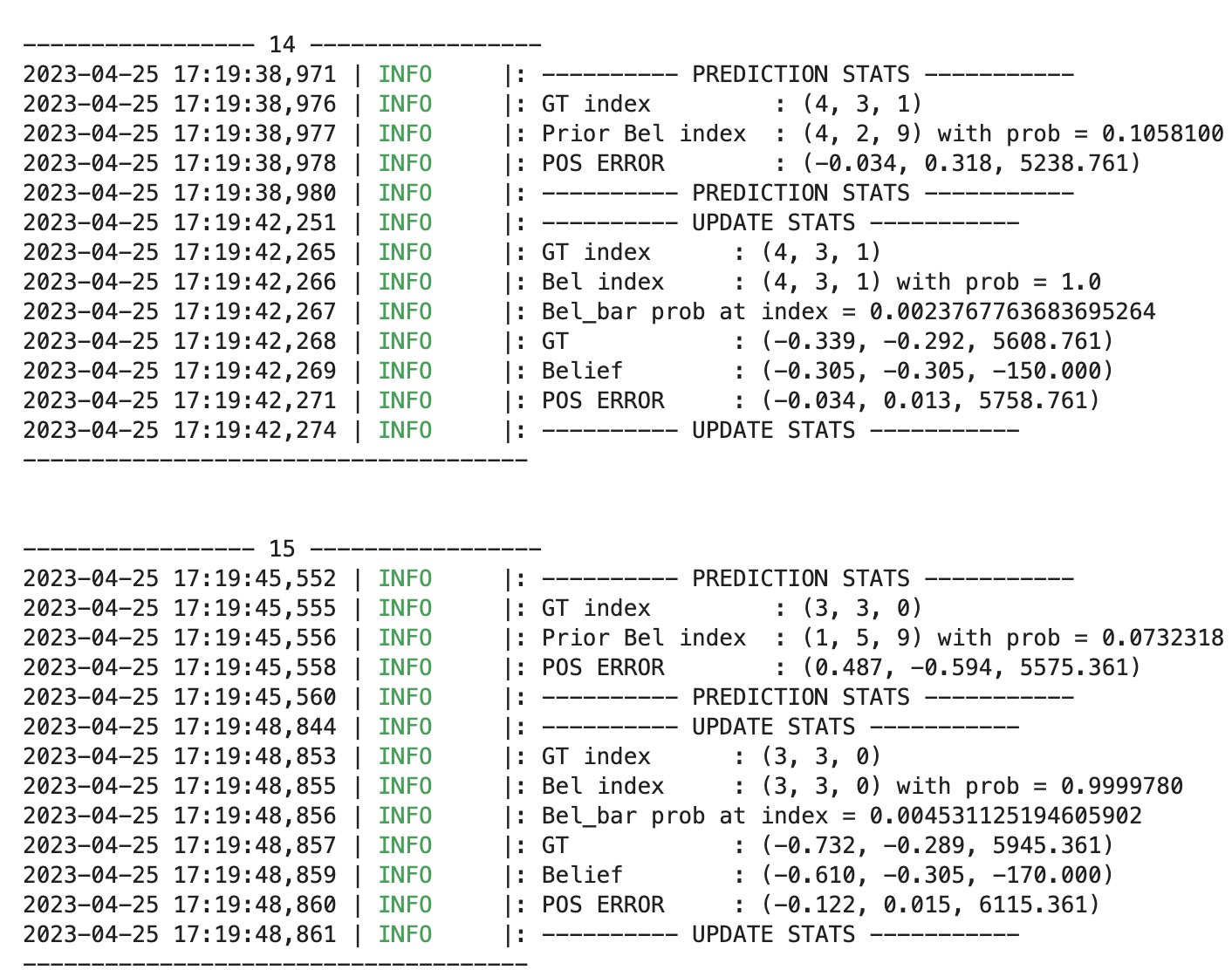
In this lab, we are required to use the Bayes filter to implement grid localization. In the pre-lab instruction, it provides us some background information and the lab description. The state of the robot is defined as (x, y, theta). The total number of cells along each axis are (12,9,18) with size of each grid cell) along the x , y and theta axes are 0.3048 m, 0.3048 meters and 20 degrees.

The Bayes filter algorithm typically involves two main steps: prediction and update. In the prediction step, the algorithm uses the prior belief, the control input data, and the system model to predict the current state of the system. This prediction incorporates the knowledge of how the system is expected to behave based on the control input data and the model. However, there is always some uncertainty associated with this prediction due to noise or inaccuracies in the model. In the update step, the algorithm uses the prediction, the observation data, and the sensor model to update the belief about the current state of the system. This update step reduces the uncertainty of the belief by incorporating the measurement data. The resulting estimate of the current state of the system is called the posterior belief. The detailed equation can be found below.

Python Code Implementation

Compute Control

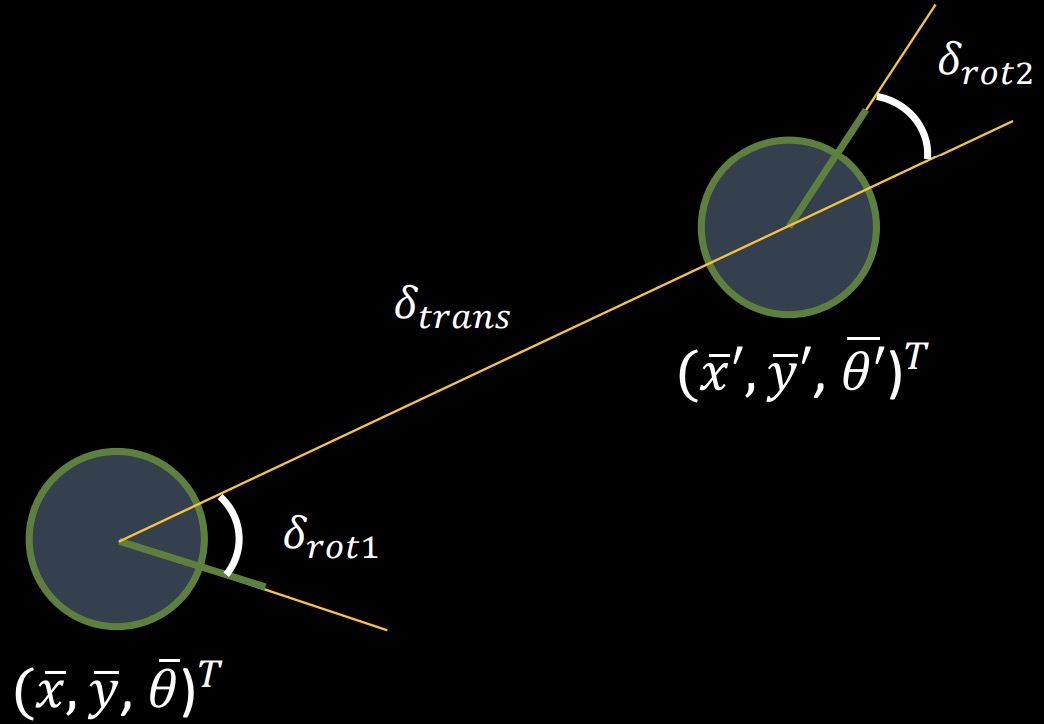
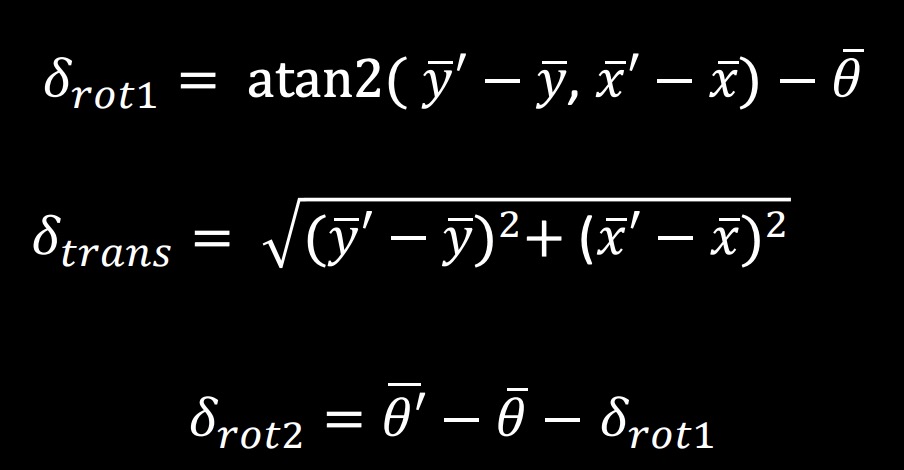
As you can see the figure and the equation provided above, both are got from the lecture materials. Those equations are directly derived from the figure with two circles and I use that to write the python code for "compute control" part. Delta_rot_1 represents the angle rotated to reach the next state. Delta_trans shows the distance that needs to move to a new cell. And Delta_rot_2 is the angle rotated to reach the final state. I first derived all the x, y, and theta value for the current and previous state and do some simple math.

Odom motion model

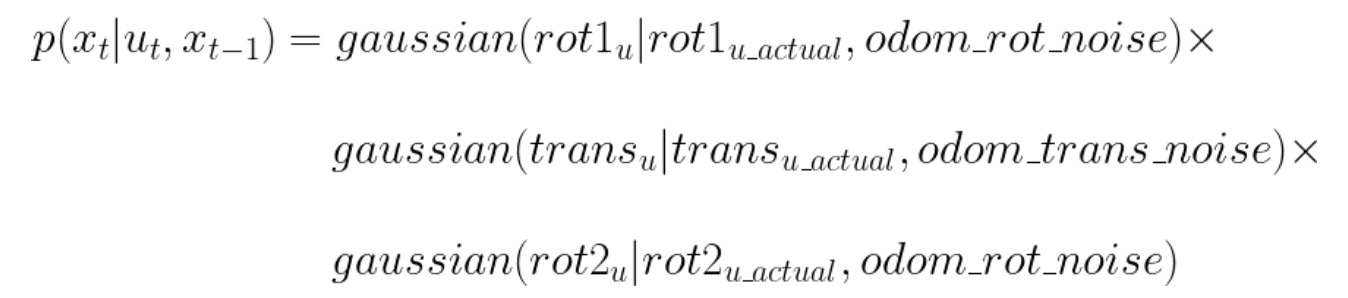
The function above is provided in the instruction for lab 10. It calculate the transition probability, which represents the likelihood that the system will transition from its current state to a new state based on the control input or action taken. The actual u is gotten in the previous step, so I just call the function "compute control". Then I can use the gaussian function to impletment the odom motion model to get the probability value. I also include the mapper.normalize_angle function to normalize my angle value.

Prediction step

In the prediction part, I also call the "compute control" function to get the cur_odom and prev_odom as the input. Here, it uses the odometer motion with current and previous pose to predict u. I use 2 sets of loop, which is 6 in total to iterate the x, y, and theta value. Because there are two many loops contains in our calculations, our calculation speed will be reduced. To avoid that, I add an if statement to ignore the belief bel value that is smaller than 0.0001.

Sensor model

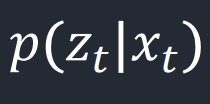
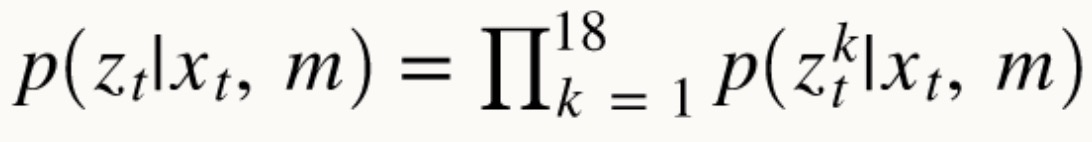
The sensor model is used to calculate the likelihood of the sensor measurements given the current state of the system. By using the equation provided in the instruction, there are 18 reading values contains in the array. The probability array can be finally calculated by using the gaussian function again with the input storing in the "loc.obs_range_data".

Update step

In the update step part, we still use the similar loop shown in the prediction part to iterate the current pose. Each loc.bel belief can be derived by multiplying the result from function "sensor model" with the bayesian prediction. Finally, we still need to normalize our value.

Video Result

Bayes filter can work in my sim robot very well. There are three lines inclued in the graph, which are the odometry values (red), the ground truth (green), and our belief (blue). The video below shows the demonstration without the bel_bar. As you can see, the belief and the ground truth are close to each other as what we want. The Odometry line contains a lot of noise, so it is reasonable to get the performance like this.

The video below shows the demonstration with the bel_bar. If the cell color is ligher, it means the it will have the higher belief.